探索世界最美方程：勾股定理脱颖而出，排行榜揭晓！

自从科学诞生以来，方程式一直是人类生产创造和各门学科不可或缺的工具。随着科学技术的飞速发展，近几个世纪以来方程式的数量更是大幅增加。可以说，人类科学的进步离不开方程式的存在。那么，有没有你所知道的方程式呢？下面就让我们一同来了解一下世界上十大最美的方程式。

世界十大最美方程式

　　《1、广义相对论方程式》是爱因斯坦的著名方程。它的内容涉及的是物理学中的重力和时空关系。广义相对论方程组描述了质量和能量如何影响时空结构，是现代宇宙学的基础。
《2、标准模型方程式》是粒子物理学的基础方程组。标准模型描述了所有已知的基本粒子及其相互作用，是物理学中最精确的理论之一，也是解释宇宙现象如核裂变、宇宙微波背景辐射的关键。
《3、微积分方程式》是微积分的基本方程。微积分方程描述了变量之间的关系，是物理学、工程学、经济学等领域的重要工具。
《4、勾股定理方程式》是几何学的基本定理。勾股定理描述了直角三角形的边长之间的关系，是解决几何问题的基础。
《5、欧拉方程式》是解析几何的基本方程。欧拉方程描述了曲线和曲面之间的关系，是解决解析几何问题的基础。
《6、狭义相对论方程式》是爱因斯坦狭义相对论的基本方程。狭义相对论描述了物体在高速运动和强重力场下的行为，是现代物理学的重要理论之一。
《7、1=0.9无限循环方程式》是一道看似无意义的方程，但它却包含了一些有趣的数学性质和物理意义。例如，它可以通过无限次迭代得到更精确的结果，这是计算机科学中的重要技巧。
《8、欧拉▪拉格朗日方程和诺特定理》是古典力学的基本方程，描述了物体的运动和力的关系。诺特定理是经典力学的基础，也是研究宇宙学、粒子物理学等领域的基础。
《9、Callan-Symanzik方程式》是计算粒子物理模型的方程组。它可以用来计算粒子的行为，是粒子物理学家的重要工具。
《10、极小曲面方程》是几何学中的一个重要问题。极小曲面是最小的曲面，是解决某些几何问题的关键。

1、广义相对论方程式

　　《1915年爱因斯坦提出的宏观物体引力理论》是爱因斯坦在狭义相对论和万有引力定律上重大的突破。在这个理论中，爱因斯坦将引力看做因物质与能量弯曲的时空，将引力与物质和能量联系起来，形成了一种全新的理论。
这一理论改变了人们对引力的理解，以前我们认为引力是一种神秘的力量，无法用科学解释。但现在我们知道，物体之间的引力是由于他们之间的物质与能量引起的时空弯曲。这种弯曲会使得物体受到一种力的作用，这种力就是我们通常所说的引力。这个理论为解释地球和其他天体的运动提供了全新的理解。
这个理论对科学的发展产生了深远的影响。它不仅为微观物理学奠定了基础，也为宏观物理学带来了革命性的改变。通过对这个理论的研究，科学家们探索出了许多新的现象和规律，例如黑洞的形成、宇宙大爆炸理论等。
此外，这个理论也推动了科技的发展。例如，GPS导航系统就是基于爱因斯坦的理论设计的。在GPS系统中，卫星会发射出时间信号，地面接收器会将这些信号与卫星发射的时间进行比较，从而确定接收器的位置。
总的来说，《1915年爱因斯坦提出的宏观物体引力理论》是一个非常重要的理论，它改变了人们对科学的理解，推动了科学的发展，为科技的发展提供了重要的理论基础。

2、标准模型方程式

　　规范对称场论是理论物理学中的一种重要理论，它描述了自然界中的三种基本力：强力、弱力和电磁力。这三种力共同维持着我们周围的世界，并且它们的性质非常特殊，以至于它们的表现方式与我们日常生活中的感觉完全不相同。
强力是物体之间的引力，是最基本的力。它可以解释物体为什么能够抵抗地球的吸引力，以及为什么星系会聚集在一起。弱力则是物体相互作用的一种力，它可以解释放射性衰变现象，以及为什么一些基本粒子可以发生相互作用。
电磁力是电子和质子之间的相互作用力，它可以解释为什么电子可以绕着原子核旋转，以及为什么物质可以产生电流。这三种力都是基本的，因为它们是所有其他力的基础。没有这三种力，我们的世界就无法存在。
规范对称场论的提出者是杨振宁和他的学生，他们使用了一种称为量子场论的数学工具，来描述这三种力。量子场论是一个强大的理论工具，它可以描述微观世界的物理现象，例如原子和粒子的行为。通过使用量子场论，杨振宁和他的学生成功地描述了这三种基本力，并且他们发现这三种力之间存在一种内在的联系。
规范对称场论的一个重要结果是它预测了希格斯粒子的存在，这是一个非常重要的研究成果。希格斯粒子是一种基本粒子，它对于理解这三种基本力的作用方式非常重要。通过观察希格斯粒子，科学家们可以更好地理解这些基本力，从而进一步推动物理学的发展。

3、微积分方程式

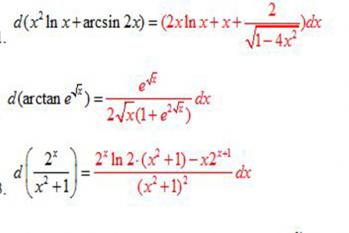
　　《微积分由牛顿和布莱尼茨两人共同创立，但因为布莱尼茨是从数学几何的角度来表述微积分，更为简单，所以现在被科学界推广使用。》的内容主要涉及微积分的创立和发展，以及其在科学领域中的广泛应用。
微积分起源于17世纪的牛顿和莱布尼茨，他们根据引力场和流体的动力学推导出了微积分的基本原理。但是，他们的阐述方式不同，牛顿更为着眼于数学符号和公式，而莱布尼茨则从几何的角度来理解和解释微积分。
尽管牛顿的数学符号和公式更加复杂，但是其对微积分的理解更为深刻和广泛。他的微积分理论不仅适用于引力场和流体动力学，也适用于很多其他领域，如物理、工程、经济、生物学等。
然而，莱布尼茨的研究成果也同样重要。他的微积分理论更为简单，易于理解和掌握，因此在科学界得到了广泛的推广和应用。尤其是在几何学和代数学领域，莱布尼茨的微积分理论起到了关键的推动作用。
总的来说，微积分的创立和发展是人类科学史上的一个重要里程碑。牛顿和莱布尼茨的贡献是不可忽视的，他们的研究成果不仅为科学研究提供了强大的工具，也为人类社会的发展带来了深远的影响。

4、勾股定理方程式

　　中国古代在几何学方面的成就举世公认，其中最具代表性的定理是著名的勾股定理。在公元前6世纪，我国古代数学家毕达哥拉斯就发现了勾股定理，他将直角三角形的三个边长分别命名为“勾”，“股”和“弦”，又将这个定理命名为“毕氏定理”。这个定理在中国古代数学中有着广泛的应用，尤其是在工程计算和建筑设计等领域。
西方古代也发现了勾股定理，但西方人进一步将这个定理提炼为一个方程式。在公元前5世纪，古希腊数学家毕达哥拉斯学派的欧几里得发现了勾股定理的方程式：a^2 + b^2 = c^2，其中a、b和c分别表示直角三角形的两条直角边的长度，而c则是斜边的长度。欧几里得的这个方程式被后人称为“毕氏方程”，它是几何学的基石之一，也是高等数学和其他学科中不可或缺的基础。
值得一提的是，虽然中国古代和西方古代都发现了勾股定理，但西方人将这个定理提炼为一个方程式，并将其应用于更广泛的领域，这在一定程度上推动了西方数学的发展。这与西方人的理性思维方式和抽象思维能力有关，他们更注重逻辑推理和符号表达，因此能够将数学定理提炼为方程式，并用它来解决更复杂的问题。
总的来说，无论是中国古代还是西方古代，都对勾股定理有着深刻的理解和应用。勾股定理是几何学的基本原理，它的发现和应用，不仅推动了古代数学的发展，也对现代科学和技术产生了深远影响。

5、欧拉方程式

　　这段文字提到了一个著名的物理方程，即欧拉方程。这个方程由瑞士数学家欧拉在18世纪提出，是流体动力学的基础之一。欧拉方程的出现，标志着微分方程在物理学中的应用得到了突破性进展。这个方程主要应用于研究无粘性流体中的运动，例如液体的流动和气体的扩散等。欧拉方程的提出，对人类对自然规律的理解和技术的发展都产生了深远的影响。

6、狭义相对论方程式

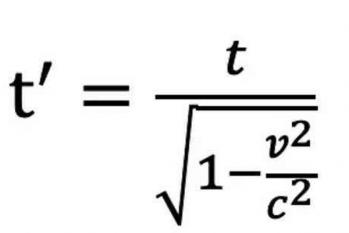
　　《发表于《论运动物体的电动力学》》是阿尔伯特·爱因斯坦在20世纪初提出的一篇重要论文，主要作用是为了修正牛顿的时空理论。在这篇论文中，爱因斯坦提出了一种新的时空观，即时间和空间并非一体的，而是可以分开的。这一理论对物理学的发展产生了深远的影响。
爱因斯坦的时空观主要是基于他对电磁现象的研究。他认为，物体在空间中的位置并非简单地由其力量决定，而是由其速度决定，而速度是由物体所带电荷和磁场决定的。因此，物体的位置和速度并非独立存在的，而是一个动态的系统，这个系统的变化会改变时空的结构。这就是爱因斯坦的相对论的核心思想。
爱因斯坦的相对论对物理学的发展产生了深远的影响。一方面，它修正了牛顿的时空理论，揭示了时间和空间的本质。另一方面，它提出了质能公式E=mc²，揭示了物质和能量的等价性。此外，相对论还为研究宇宙的起源和演化提供了新的框架。
总的来说，爱因斯坦通过《发表于《论运动物体的电动力学》》提出了一种新的时空观，这个观点对物理学的发展产生了深远的影响。它揭示了时间和空间的本质，提出了质能公式，为研究宇宙的起源和演化提供了新的框架。

7、1=0.9无限循环方程式

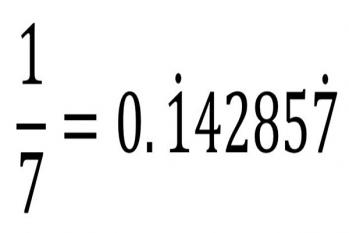
　　康奈尔大学的数学家史蒂文提出的这个方程，是他在数学领域的又一重大发现。这个方程的左侧代表了一个数字的开始，右侧则代表了无限循环，这意味着这个数字无限趋近于1。这个方程的意义深远，它揭示了数学中的许多重要规律。
首先，这个方程揭示了数学中的无限级数，它可以用来计算诸如π和e等无限级数。这些无限级数是数学中的重要概念，它们在物理、工程和计算机科学等领域都有广泛的应用。
其次，这个方程也揭示了数学中的极限概念。无限级数往往不能直接求解，但是通过计算每个项的极限，我们可以得出无限级数的和。这就是数学中的极限概念，它在微积分和其他分支的数学中都有重要的应用。
最后，这个方程还揭示了数学中的连续性和离散性。数字的开始可以看作是连续的过程，而无限循环则可以看作是离散的过程。这两种过程在数学中有重要的联系，它们可以帮助我们理解许多数学现象。
总的来说，康奈尔大学的数学家史蒂文提出的这个方程，虽然简单，但却蕴含了深刻的数学原理和规律。它的发现，对数学的发展和应用起到了重要的推动作用。

8、欧拉▪拉格朗日方程和诺特定理

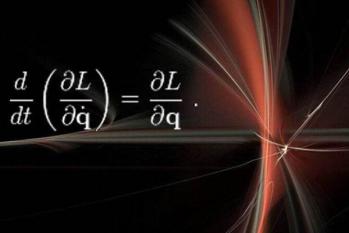
　　在理论物理中，这是一个非常重要的概念，涉及到广义相对论和粒子物理学。
广义相对论，是爱因斯坦创立的一种关于引力的理论，描述了时空的弯曲，以及物体如何受到这种弯曲的影响。其中的核心原理之一就是保持了一个重要的数学关系，即黎曼张量不变性。这个原理保证了广义相对论的预测是稳定的，不会因为微小的变化而改变。
粒子物理学是研究宇宙中最基本的粒子和它们相互作用的学科。在粒子物理学中，有一些守恒定律是必须遵守的，包括能量守恒、动量守恒、角动量守恒等。这些守恒定律能够帮助我们理解和预测粒子的行为。
对称性是物理学中非常重要的一个概念，它指的是一种对物理系统进行变换后，系统不变的性质。一般情况下，物理系统只有局部对称性和全局对称性。局部对称性是指系统在某一局部区域发生变化时，系统在其他区域保持不变；全局对称性是指系统在所有区域发生变化时，系统保持不变。
把连续对称性和守恒定律联系起来，我们可以看到，它们表示的是相同的数学关系。当我们对一个物理系统进行变换，如果这个变换能够保持系统的连续对称性，那么系统就仍然遵守所有的守恒定律。反过来，如果一个物理系统遵守所有的守恒定律，那么这个系统就具有连续对称性。
因此，理论物理的中心结果之一，表达了连续对称性和守恒定律的一一对应，对于所有基于作用量原理的物理定律是成立的。这个原理是物理学中非常重要的一个基础，对于理解和预测物理现象具有重要的意义。

9、Callan-Symanzik方程式

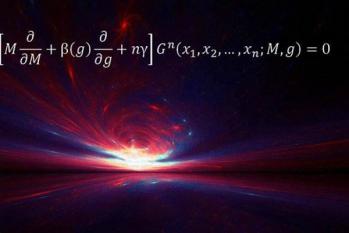
　　斯特拉斯提出来的方程，被后人称为斯特拉斯克方程，是物理学领域中的一个重要方程，它描述的是质子和中子内部的电荷分布和动量分布。斯特拉斯克方程的提出，为理解和预测原子核的行为提供了理论基础，使得物理学家能够更准确地估算出质子和中子的质量和大小。
质子和中子是构成原子核的两种基本粒子，它们具有极高的密度和极强的相互作用力。斯特拉斯克方程，通过描述质子和中子的电荷分布和动量分布，揭示了它们内部的能量结构，从而得出其质量。
此外，斯特拉斯克方程还能应用于许多其他领域，例如核物理、粒子物理、凝聚态物理和量子力学等。例如，通过解析斯特拉斯克方程，物理学家可以计算出原子核的能量，从而揭示它的稳定性和反应性。
斯特拉斯克方程的提出，不仅推动了物理学的发展，也对人类理解物质的本质和宇宙的构造提供了重要线索。

10、极小曲面方程

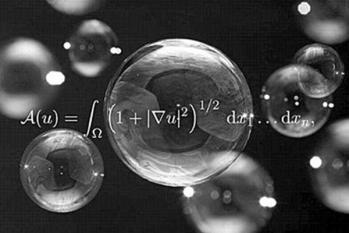
　　极小曲面，也被称为极小曲线，是指平均曲率为零的曲线。这个概念在几何学中有重要应用，尤其在微分几何和拓扑学中。
平均曲率是衡量曲面形状的一种方式。一个曲面的平均曲率就是所有点周围的切线的平均曲率。如果一个曲面的平均曲率总是为零，那么这个曲面就是极小曲面。
极小曲面在很多应用中都有重要地位。例如，它们在物理中的应用最为广泛，因为许多自然现象，如流体的流动，都涉及到极小曲面。在工程中，极小曲面也被用来设计和分析结构，因为它们可以保持形状的稳定和均匀。
此外，极小曲面也在电子显微镜的分析中起着关键作用。在电子显微镜中，研究人员观察的是微小的晶体结构，这些结构通常是由极小曲面组成的。通过分析这些曲面，研究人员可以理解晶体的结构和性质。
总的来说，极小曲面是一种描述几何形状的数学工具，它在多个领域都有重要应用，包括物理、工程和材料科学等。