揭秘世界十大推理计算公式排行榜，你学过哪些？

在自然科学领域中，公式是用数学符号表示变量之间关系的表达式，具有普适性，可应用于各类问题。在数理逻辑中，公式是表达命题的形式语法对象，其命题的真假可能依赖于自由变量的值，公式在不同的逻辑系统中的定义有所不同。以下是全球十大推理计算公式：
1. 贝叶斯定理：解释了在给定证据的情况下，事件（或参数）的先验概率如何影响其后验概率。
2. 欧拉公式：将复数指数函数的导数与实数的积分结合在一起，以便在复数域中进行计算。
3. 拉格朗日乘子法：一种优化方法，用于找到函数的最小值和最大值。
4. 费马大定理：证明了当n大于2时，不存在正整数x、y和z满足x^n + y^n = z^n。
5. 卡尔丹公式：推导出Euler $\Phi$ 函数，它是离散数论中的重要工具，用于计算模数为p的数的约数个数。
6. 欧拉公式：将复数指数函数的导数与实数的积分结合在一起，以便在复数域中进行计算。
7. 极限定理：根据误差函数的连续性和一致性和局部可微性，可以推导出极限的性质。
8. 奇特的积分公式：包括Riemann积分、黎曼积分和Lebesgue积分等，用于计算和分析函数在不同积分区间上的积分。
9. 柯西积分公式（Cauchy积分公式）：一种特殊的黎曼积分公式，用于求解常微分方程。
10. 巴勒綮斯公式：描述了数列和的组合性质，以及复数和的组合性质，被认为是数列理论中的一个重要工具。

TOP 1、傅立叶变换

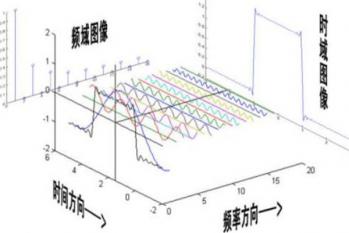
　　傅立叶变换是一门数学工具，它在许多领域都有广泛的应用，包括但不限于信息处理、信号处理、数字信号处理、图像处理、音频处理等等。
首先，傅立叶变换在数字频率领域有着重要的作用。它可以帮助我们理解和分析信号的频谱特性。通过傅立叶变换，我们可以将一个时间序列信号转换为频域信号，从而更好地理解信号的频率特性和能量分布。
其次，傅立叶变换还支持任何不规则信号的变换。这意味着它可以处理各种各样的信号，包括声音、图像、视频等。它可以将复杂、不规则的信号转换为易于理解和处理的频域信号。
除了在数字频率领域的应用，傅立叶变换还在许多其他领域有着广泛的应用。例如，在计算机科学中，傅立叶变换被用于图像和视频处理，以便提高图像和视频的质量。在工程领域，傅立叶变换被用于电路分析，以便模拟和分析电路的行为。在物理学中，傅立叶变换被用于研究波动和振动，以便理解物理现象的本质。
总的来说，傅立叶变换是一种强大的数学工具，它在许多领域都有着广泛的应用。尽管它可能看起来复杂，但是只要我们掌握了基本的概念和原理，就能有效地使用它来解决我们的问题。

TOP 2、1+1=2

　　《1+1=2》这个公式在数学领域的重要性无需过多强调，争议不断，思考不休。这个公式所涵盖的知识领域很广泛，包括基础数学、高等数学、逻辑学、哲学等多个领域。
基础数学角度，《1+1=2》是加法的基本原理，它揭示了两个物体之间相加的关系，是基本的数学概念和技能。
高等数学角度，《1+1=2》是一个非常基础的数学事实，也是数学思维的基础。在高等数学中，它被用于证明许多更复杂的数学定理，如费马大定理等。
逻辑学角度，《1+1=2》是逻辑推理的基石。在逻辑学中，它被用于证明一系列基本的逻辑规则，如二元运算定律等。
哲学角度，《1+1=2》是一个哲学问题，涉及到对现实世界认识的理解，以及对真理的定义。哲学家通过争论和思考，试图理解这个看似简单的问题。
总的来说，《1+1=2》是一个简单而深远的公式，它不仅在数学领域起着重要的作用，也在其他领域产生了深远的影响。

TOP 3、毕达哥拉斯定理

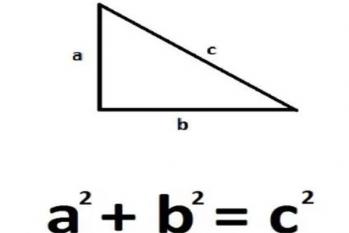
　　毕达哥拉斯定理，又称为勾股定理，是古希腊数学家毕达哥拉斯在公元前6世纪提出的一项基本几何定理。这个定理指出，在一个直角三角形中，直角边的平方之和等于斜边的平方。也就是说，如果一个三角形的两条直角边的长度分别为a和b，斜边的长度为c，那么a² + b² = c²。
这个定理的证明方法其实有很多种，其中一种是通过构建直角三角形，然后利用勾股定理的性质进行计算和证明。例如，我们可以将一个直角三角形分成两个小直角三角形，然后使用勾股定理的性质，将每一个小直角三角形的短直角边的平方和和斜边的平方相加，再将结果相加，得到整个直角三角形的斜边的平方。
另外，毕达哥拉斯定理也可以通过几何迭代的方法进行证明。这种方法基于一个基本的原理：任何图形都可以通过不断的分割和组合，最终得到一个由两个等边三角形组成的图形。在这些等边三角形中，每一条边的长度都是相等的，因此，它们的平方和也是相等的。将这些等边三角形组合成一个四边形，然后通过一些简单的计算，就可以得到直角三角形的斜边的平方。
无论使用哪种方法证明毕达哥拉斯定理，都需要一些基本的几何知识和计算能力。然而，一旦掌握了这个定理，就可以解决许多复杂的几何问题，包括计算三角形的边长，测量物体之间的距离，以及设计和构建各种形状的图形等等。
总的来说，毕达哥拉斯定理是一项非常重要的几何定理，它不仅在古希腊时期就得到了广泛应用，而且在现代数学中仍然发挥着重要的作用。通过学习和理解毕达哥拉斯定理，我们可以更好地理解和解决问题，帮助我们更好地理解和欣赏这个世界的美丽和复杂性。

TOP 4、麦克斯韦方程组

　　这篇文章可能会涉及到电磁学、物理学、数学等多个领域。
首先，麦克斯韦方程组是电磁学领域的基础理论，由詹姆斯·麦克斯韦在19世纪提出。这个方程组包含了电荷、电场、磁场、电磁波等物理量之间的关系，是描述电磁现象的基本工具。
其次，麦克斯韦方程组对现代社会文明的贡献巨大。例如，它是电能的转换、交流电的产生和传输、无线通信等现代科技的基础。没有麦克斯韦方程组，我们不可能发明和使用这些科技产品，现代社会的文明程度也会大大降低。
再次，麦克斯韦方程组的完美性和一致性得到了广泛的认可。它的每一个方程都体现了物理现象的精确性和严密性，没有任何明显的漏洞或矛盾。这也是为什么人们评价说，如果没有麦克斯韦方程组就没有现代社会的文明。
最后，麦克斯韦方程组是一个复杂的数学模型，包含了大量的物理量和数学运算。要理解和掌握这个方程组，需要深厚的物理、数学和计算机科学知识。这也是为什么说，麦克斯韦方程组是完美到无可挑剔的，可以说宇宙间的任何电磁用这个方程组都能很好的被解释。

TOP 5、欧拉公式

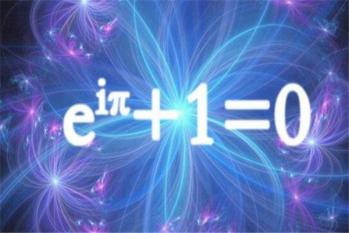
　　　　这个欧拉公式从形式上看非常的巧妙，没有任何多余的“杂质”，数学家们评论说凡是第一眼爱上这个公式的人必定会成为数学家，可见该公式的伟大之处。

TOP 6、质能方程

　　《质能方程》是世界上最伟大的十大公式之一，由物理学家阿尔伯特·爱因斯坦在他的相对论中提出。这个公式是E=mc²，其中E代表能量，m代表质量，c代表光速。
这个公式揭示了质量和能量之间的关系，也就是物质和能量是可以相互转化的。在高能状态，物质可以转化成能量，反之亦然。这不仅改变了我们对物质和能量的理解，也为现代科学技术的发展提供了理论基础。
质能方程在核能领域有着重要应用。我们知道，原子弹和氢弹主要是通过核裂变或核聚变产生巨大的能量。而质能方程告诉我们，这是因为在核反应中物质的质量发生了变化，转化为大量的能量。这种方法被广泛应用于各种高科技领域，如核电站、核武器、医疗等。
随着科技的进步，质能方程的应用将更加广泛。例如，随着量子计算机的发展，人们可能可以利用质能方程实现更高效的能量转换。同时，通过研究质能方程，我们也可以更好地理解宇宙的本质，探索更广阔的宇宙。
总的来说，质能方程是现代物理学和科技的重要基础，它的出现和发展，极大地推动了人类科技进步的步伐，也为我们揭示了宇宙的奥秘。

TOP 7、德布罗意方程组

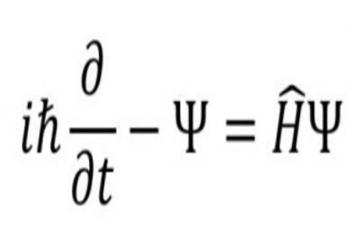
　　波粒二象性是量子力学的基本原理之一，它指出微观粒子，如电子、光子和质子等，既可以表现出粒子的特性，也可以表现出波动的特性。德布罗意把这种现象归结为物质的波粒二象性，他的理论是通过对光的波粒二象性的研究得来的。德布罗意方程组是由德布罗意提出的，它描述了光的波粒二象性。这个方程组表明，光的波长与它的能量之间存在着直接的关系。德布罗意的理论解释了光的波长和能量之间的关系，并且为波粒二象性的研究开辟了新的方向。他的研究成果在1929年被诺贝尔物理奖委员会认可，德布罗意因此获得了诺贝尔物理学奖。

TOP 8、圆的周长公式

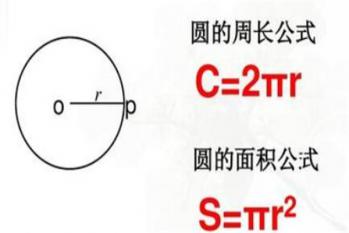
　　如果您需要创作一篇关于“计算太阳系包起来的周长”的文章，您可以考虑以下的一些相关领域知识：
1. 太阳系的基本构成：太阳系包括八大行星（水星、金星、地球、火星、木星、土星、天王星、海王星）、矮行星和其他小天体。每个行星都有其独特的大小和形状，因此太阳系的总体周长会因各个行星的距离和形状而有所不同。
2. 宇宙学的基本概念：宇宙学是研究宇宙的起源、结构、演化和未来命运的科学。在宇宙学中，我们通常使用球体来描述宇宙，因为宇宙的形状似乎是一个无限大的球体。
3. 预测天体现象的科学方法：预测天体现象的科学方法主要包括数学建模和数值模拟。数学建模是一种将物理和数学原理应用于实际问题的方法，数值模拟则是一种通过计算机进行大规模数据运算以预测物理现象的方法。
4. 误差分析：误差分析是一种评估测量结果与真实值之间差异的方法。对于太阳系包起来的周长的计算，我们需要考虑到不同行星的距离和形状，以及计算过程中可能出现的误差。
5.科学知识与文学知识的结合：您还可以尝试将科学知识与文学知识相结合，以提高文章的吸引力和趣味性。例如，您可以将太阳系比作一个巨大的小球，地球就像是其中的一颗小沙粒，而包起来的周长就像是小球上的金色链条。
希望以上的内容能够对您的文章创作有所帮助。

TOP 9、牛顿第二定律

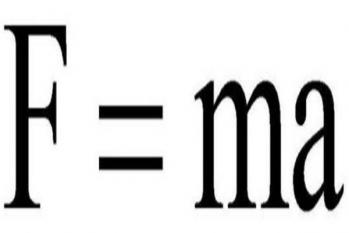
　　这段文字提到了牛顿第二定律，这是物理学中的一个重要公式，它的出现是物理学研究的重要里程碑。牛顿第二定律描述了物体的运动状态如何受到外力的影响，它是我们理解物理世界的基本工具。
牛顿第二定律的数学表达式为F=ma，其中F代表作用在物体上的力，m代表物体的质量，a代表物体的加速度。这个公式表明，物体的加速度与作用在它上面的力成正比，与它的质量成反比。
牛顿第二定律的出现，让我们可以使用数学方法来描述和预测物体的运动。这是物理学的一个重大突破，因为它将物理学从定性研究带到了定量研究。通过解析牛顿第二定律，我们可以得到许多重要的物理公式，例如动量守恒定律、动能定理等。
同时，牛顿第二定律也是许多其他物理学公式的基础，例如万有引力定律。许多现代科学和技术，如航空航天、工程设计等，都离不开牛顿第二定律的指导。
因此，牛顿第二定律可以说是物理学研究的基石，它的重要性无法夸大。学习上许多物理方程都需要用牛顿第二定律导出。

TOP 10、薛定谔方程

　　薛定谔方程是量子力学的基本方程，它描述了微观粒子的量子态随时间的演化。薛定谔方程的提出，不仅揭示了力学中位移和速度的关系，而且使我们能够理解微观粒子的行为和性质，对于现代科技的发展具有极为重要的意义。
薛定谔方程的表达式为：iħ ∂ψ/∂t = Hψ，其中i是虚数单位，ħ是约化普朗克常数，ψ是一个复数函数，代表量子系统的状态，H是哈密顿量，代表系统的总能量。
薛定谔方程的提出开创了量子力学的新纪元，它的数学形式使得我们可以定量地描述和预测微观粒子的行为。这个公式在物理学的应用极为广泛，例如在原子物理学、分子物理学、固体物理学、凝聚态物理学等领域都有重要应用。
另外，薛定谔方程的解，也就是量子态，揭示了微观粒子的波粒二象性。这意味着，微观粒子既具有波动的特性，又具有粒子的特性，这是经典物理所无法解释的。
总的来说，薛定谔方程在物理学中有着深远的影响，对于现代科技的发展和人类对自然世界的理解都有着重要的贡献。