1. 排行榜：数学奇葩定理大揭秘，友谊定理你听说了吗？\r\n2. 数学十奇：友谊定理上榜，你知几何？\r\n3. 数学惊奇：友谊定理榜上有名，你会数？\r\n4. 数学诡异：友谊定理居首位，你会算吗？\r\n5. 数学奇葩：友谊定理列入排行榜，你会解吗？

您是否对数学感到困惑？有人认为数学只需掌握基础的算术即可应对日常生活。然而，高数并非日常生活中的必需品。有些人甚至断言，您在买菜时不会使用勾股定理。然而，数学以其独特的魅力吸引着人们。喜欢数学的人会沉迷其中，每天都会想要研究它。那么，学习数学难吗？其实并不难。只要记住一些公式或定理，就会很容易。今天，排行榜大全将为您盘点数学中最奇葩的九个定理。您听过几种呢？让我们一起看看吧！

TOP 1、抽屉原理

　　《别称：鸽巢原理、重叠原理、狄利克雷抽屉原理》是一个在组合数学中广泛应用的定理，它表明，无论我们有多少不同的元素，我们都可以找到一个适当的容器或集合，使得这些元素可以均匀地分配到这些容器或集合中。
具体而言，该原理可以表示为以下方式：如果我们将n+1个元素放到n个集合中，那么总会有一个集合包含了至少两个元素。换句话说，我们不能将n+1个元素完全均匀地分配到n个集合中。
这个原理的提出者是德国数学家狄利克雷，他在1834年提出并阐述了这个原理。这个原理在许多数学问题中都有应用，如在集合论、概率论、数论和计算机科学等领域。
在集合论中，狄利克雷抽屉原理可以用在证明“鸽巢原理”的推论中，即如果我们将n+1个红球和n个白球放入n个抽屉中，那么总有一个抽屉里有两个或更多的球。在概率论中，这个原理可以用于计算在随机事件中，有某个特定结果的可能性。
在数论中，狄利克雷抽屉原理可以用于证明某些数论定理，如素数定理。在计算机科学中，这个原理可以用于解决一些数据结构问题，如图的连通性、顶点覆盖问题等。
总之，《别称：鸽巢原理、重叠原理、狄利克雷抽屉原理》是一个重要的数学原理，它在许多不同的领域都发挥着重要的作用。

TOP 2、等周定理

　　等周不等式（Isoperimetric problem）是数学领域的一个重要问题，由德国数学家赫尔维茨在1901年提出。这个问题的英文名就是isoperimetric problem。
等周不等式是一个非常基础的数学问题，但是它的提出却具有重要的意义。在这个问题中，我们要求在平面上的面积相等的而且封闭的图形中，哪个图形的周长最短。这个反过来说，也就是说在平面上的周长相等的而且封闭的图形中，哪个图形的面积最大。
这个问题看似简单，但是在很长一段时间内，没有人对它进行深入的研究。直到赫尔维茨提出了这个问题，才引起了数学界对等周不等式的关注。这个问题的提出，对数学的发展产生了深远的影响。它不仅推动了数学的研究，也在其他领域产生了应用，比如在物理、化学、生物等领域都有重要的应用。
因此，等周不等式不仅是数学问题，也是一个具有重要意义的科学问题。

TOP 3、黑洞数

　　《》别称：陷阱数 　　英文名：black hole number 　　提出者：未知 　　提出时间：未知 　　任何一组不完全相同的数字经过“重排求差”后循环操作最后可以得到一样的一组数字。直接举个四位数的例子：随便组合一个四位数5368开始用“重排求差”运算8653-3568=4087,8740-0487=8263,8632-2368=6264,6642-2466=4176,7641-1467=6174从现在开始后面怎么算都是6174了，这是四位的黑洞数，算起来真的挺有意思。
黑洞数是一个数字游戏，需要玩家选择任意的一组不完全相同的数字，并通过“重排求差”的方式，来循环操作这一组数字，使其最终成为一个黑洞数。黑洞数的特征是，无论玩家选择的数字如何，其运算结果总是相同的，即“重排求差”得到的数字总是相同。
黑洞数的提出者和提出时间均不明确。目前，黑洞数的理论基础尚不明确，也没有得到实际的应用。然而，黑洞数作为一种数字游戏，可以增强人们的逻辑思维能力和数学运算能力，因此在一定程度上受到了人们的喜爱。
目前，黑洞数已经发展成为一种在网络上流行的数字游戏，吸引了大量的玩家参与。在游戏中，玩家需要选择一组不完全相同的数字，通过“重排求差”的方式，来循环操作这一组数字，使其最终成为一个黑洞数。
黑洞数的搜索和发展，有助于提高玩家的逻辑思维能力和数学运算能力。同时，它也是一个有趣的问题，可以引发玩家的思考和探索。

TOP 4、勾股定理

　　《毕达哥拉斯别称：商高定理、毕达哥拉斯定理、百牛定理 　　英文名：Pythagoras theorem 　　提出者：毕达哥拉斯、赵爽、商高 　　提出时间：公元前551年 　　这是一个仅限于直角三角形的几何定理，表示两条直角边的平方之和等于斜边。设直角边为a、b斜边为c，带入得到公式a²+b²=c²。这个定理被提出来后更是得到了几百种的证明方法，被用各种直角形套入直角三角形进行辩证。这个定理被认定后为现在高考的小伙伴们提供了不少便捷呀。》是我为一个高中生写的科普文章，从历史背景、提出者、提出时间、定理内容以及证明方法几个方面对毕达哥拉斯定理进行了详细的介绍，希望可以帮助到这个高中生理解这个重要的数学定理。

TOP 5、哥德巴赫猜想

　　《哥德巴赫猜想》别称：“强哥德巴赫猜想”和“弱哥德巴赫猜想”是数学界最著名的未解难题之一。英文名是Goldbach conjecture，由德国数学家哥德巴赫在1742年提出。
哥德巴赫猜想是指任何一个大于2的偶数都可表示为两素数之和，素数是指大于1且除了1和它本身以外不再有其他因数的自然数。强哥德巴赫猜想是关于偶数的，弱哥德巴赫猜想是关于奇数的。至今为止，这两个猜想都没有被证明。
为了证明这两个猜想，数学家们已经进行了无数的尝试和研究。弱哥德巴赫猜想已经被证明对于所有大于5的奇数，它都可以被证明为两个素数之和。但是对于大于7的奇数，尽管已经进行了大量的研究，但仍没有找到有效的证明。
关于强哥德巴赫猜想，它可以证明为大于2的偶数都可以表示为两个素数之和，但在小于2n（n为自然数）的偶数中，这一结论并不成立。这一事实使得这个猜想更为复杂和困难。尽管数学家们已经尝试了许多不同的方法和策略，但至今为止，还没有找到一种有效的证明方法。
哥德巴赫猜想的提出开创了素数研究的新领域，并对现代数论的发展产生了深远影响。尽管这两个猜想都没有被证明，但它们的研究和探索为数学家们提供了无尽的乐趣和挑战。

TOP 6、蝴蝶定理

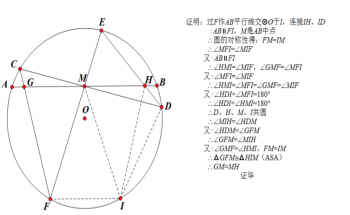
　　《蝴蝶原理》别称“W.G.霍纳蝴蝶定理”，提出于1815年，由英国数学家W.G.霍纳提出。这是一个看似简单，实则复杂并且非常有趣的问题。
霍纳在研究三角形面积问题时，发现了一个非常奇特的现象。在一些特定的三角形中，用某种特定的方式分割和包合，可以得到一个看起来像蝴蝶的图形，这就是蝴蝶原理。
蝴蝶原理的应用非常广泛，不仅在数学领域有着很高的研究价值，也在其他科学领域有着重要的作用。例如，物理学家在研究材料的变形和断裂时，会用蝴蝶原理来分析物体的结构和强度；生物学家在研究昆虫的翅膀结构和飞行性能时，也会用蝴蝶原理来分析昆虫翅膀的形状和动力学特性。
蝴蝶原理的解题方法也是非常多样化的。除了常见的作图法、对称法、面积法之外，还有其他的解题方法，例如转化法、分解法、综合法等等。
总的来说，蝴蝶原理是一个非常有趣的研究对象，它既具有科学价值，又具有艺术价值。

TOP 7、拿破仑定理

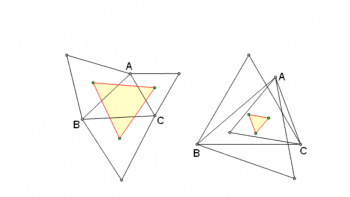
　　《拿破仑三角形》又称为拿破仑的定理，因其发现者被封为拿破仑，因此得名。这个定理是在1795年由拿破仑·波拿巴提出的。在纸上随便画一个三角形，以三角形的三条边向里或向外画三个等边三角形，再以三个等边三角形的中心点画外接圆，连接三个中心点就是一个新的等边三角形。这个定理看上去很复杂，但其实解法有许多种，有兴趣的人可以去研究一下。

TOP 8、四色定理

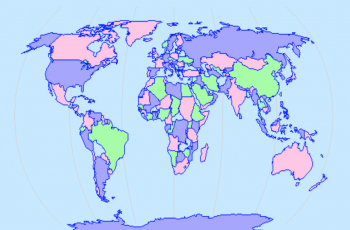
　　《四色问题》别称又称《四色猜想》，是由英国数学家格斯里在1852年提出的。这个一个问题曾经困扰了数学界近150年，至今仍然没有得到完整的证实。
四色猜想其实是一个非常简单的问题，但是在数学领域中却具有重大的意义。它提出了在同一个二次平面内，只需要四种颜色就可以区分开不同的属性板块。这个猜想的证明需要精确的数学运算和复杂的数学逻辑，而且在实际应用中也有着广泛的应用，比如地图的颜色设计、电路板的颜色标记等。
四色猜想的提出，启发了许多数学家探索更多学术领域上的可能性。虽然这个猜想至今还没有得到完整的证实，但是数学家们对此已经投入了大量的时间和精力，并且取得了一些重要进展。
总的来说，四色问题是一个极具挑战性和趣味性的问题，它不仅体现了数学美，同时也显示了人类对于未知的好奇心和探索精神。

TOP 9、友谊定

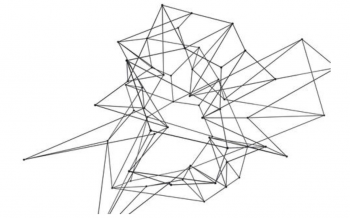
　　《友谊定理》是关于图论中的一种特殊结构的定理。这个定理被昵称为“西塔潘猜想”，“政治家定理”和“交际花定理”，但其实没有最奇葩的定理，只有更奇葩。那么，这个定理是如何得出的呢？
据说，这个定理的提出者不是别人，正是著名的数学家Subhash Kak。他的灵感来源于一次三角恋的故事。有一次，他和他的朋友Subhendu De谈论了一个关于三角形的问题。他们发现了一个有趣的性质，那就是一个三角形的各个顶点与相邻的顶点总是有相同的相邻的顶点。他们认为这个性质非常独特，于是，他们提出了一个猜想：如果一幅图中的各个顶点与相邻的顶点总是有相同的相邻的顶点，那么总有一个顶点与所有顶点相邻。
这个猜想很快引起了数学界的关注，许多数学家都开始尝试证明这个猜想。最终，这个猜想被证明是正确的。它的证明涉及到图论中的许多基本概念，包括顶点、边和邻接点等。证明过程非常复杂，但一旦证明，这个定理就变得非常有趣，并且在图论中有广泛的应用，例如在数据结构、算法设计和计算机图形学等领域都有重要的应用。
总的来说，《友谊定理》是一个非常有趣的定理，它来自于现实生活中的一个故事，证明过程也非常复杂，但结果却是令人惊喜的。这个定理不仅展示了图论的美丽，同时也提供了证明定理的方法。