数学排行榜：揭秘九大定理，除了勾股定理，还有哪些你知道？最后一个最奇葩

《数学其实是一门很有趣味的学科，相信很多人还没有发掘出它的乐趣所在。比如说三的倍数特征，你知道多少人主动发现了这个小规律吗？现在的我们觉得，基础的数学知识其实是前人经过反复验证才得出的理论，接下来就让我们一起看看数学的九个定理吧。

数学的九个定理

　　1. 抽屉原理：这是一个基本的数学原理，它表明如果有n个不同的物品，放入k个抽屉中，至少有一个抽屉里会有2个或更多的物品。这个原理在优化问题、组合数学、概率论等领域都有广泛的应用。
2. 等周定理：这个定理是关于三角形的一个定理，它表明一个三角形的内角总和等于180度，而三条边的长度之和总是等于定值。这个定理在几何学、三角学等领域都有重要的应用。
3. 黑洞数：这是指在特定的数列中，如果一个数等于它的所有前一项的和除以2，那么这个数就是黑洞数。这个数列被用来模拟黑洞的行为，它的研究涉及到数论、科学数学等领域。
4. 勾股定理：这是一个古老的数论定理，它表明在一个直角三角形中，直角边的平方和等于斜边的平方。这个定理在几何学、代数学等领域都有广泛的应用。
5. 哥德巴赫猜想：这是一个著名的数学猜想，它表明所有大于2的偶数都可以表示为两个质数之和。这个猜想在数论、计算机科学等领域都有重要的影响。
6. 蝴蝶定理：这是一个关于数学模型的定理，它表明在一个复杂的社会系统中，一个小的事件可能会引发一个大的连锁反应，就像蝴蝶效应一样。这个定理在社会学、经济学等领域都有重要的应用。
7. 拿破仑定理：这个定理是一个关于抛物线的定理，它表明对于任何一条通过原点的抛物线，它的切线总不会包含任何一点。这个定理在几何学、数学分析等领域都有重要的应用。
8. 四色定理：这是一个著名的平面图着色定理，它表明任何平面图都可以用四种颜色进行着色，使得相邻的两个区域的颜色不同。这个定理在计算机科学、数学理论等领域都有重要的影响。
9. 友谊定理：这个定理是一个关于社交网络的定理，它表明在一个社交网络中，任意两个不相邻的人至少可以通过一个共同的朋友联系起来。这个定理在社会学、网络科学等领域都有重要的应用。

1、抽屉原理

　　狄利克雷原理，又称鸽巢原理、重叠原理，是组合数学中的一个基本定理。该定理指出，如果有一个大于等于n的集合中的元素被分别放在n个集合中，那么必定存在一个集合至少包含两个相同的元素。
这个原理广泛应用于各种数学问题中，例如在概率论中，如果从一个包含n个元素的集合中随机抽取k个元素，那么至少有两个元素是相同的概率是1-1/((n+k-1)! / (n!*(k-1)!))。在组合数学中，可以使用狄利克雷原理来计算一些组合问题，例如求解组合数、排列数等。
狄利克雷原理也与计算机科学有关。在数据结构和算法中，人们经常使用鸽巢原理来设计算法，例如在排序算法中，可以使用鸽巢原理来判断是否已经包含了一个元素在正确的位置上。在计算机网络中，也可以使用鸽巢原理来处理路由选择等问题。
狄利克雷原理的应用非常广泛，不仅在数学中，在其他领域也有很多应用。例如在物理学中，可以使用狄利克雷原理来分析粒子在磁场中的运动；在经济学中，可以使用狄利克雷原理来分析市场供求关系；在生物学中，可以使用狄利克雷原理来分析种群的动态等等。

2、等周定理

　　《等周问题》又被称为等周不等式，是由当时的统计学家赫尔维茨在1901年提出的。这个问题看起来似乎很简单，但在当时，却引起了他的极大兴趣和研究。
等周问题源于赫尔维茨对统计学的探索，他试图找到一个最优解来解决计算面积的方法。他认为，在平面上的面积相等的而且封闭的图形中，圆的面积最大。这个观察引发了他对于等周问题的研究，他想要找出一个度量图形形状的方法，使得面积相等的图形的周长相等。
通过精心的计算和实验，赫尔维茨发现，实际上在平面上的周长相等的而且封闭的图形中，圆的面积是最大的。这一结论在当时引起了学术界的轰动，因为它表明了数学和物理之间的联系，以及数学在实际问题中的应用。
等周问题的提出，对现代数学的发展产生了深远的影响，特别是对几何学和几何分析的发展。它不仅是对数理解几何形状的一种方法，也是研究和解决问题的重要工具。在数学、物理、工程和其他许多领域，等周问题都得到了广泛的应用。

3、黑洞数

　　《黑洞数》别称“陷阱数”英文名为“black hole number”，提出者和提出时间未知。黑洞数是指任何一组不完全相同的数字经过“重排求差”后循环操作最后可以得到一样的一组数字。
例如，我们随便组合一个四位数5368，用“重排求差”运算8653-3568=4087，8740-0487=8263，8632-2368=6264，6642-2466=4176，7641-1467=6174。从现在开始后面怎么算都是6174了，这是四位的黑洞数，算起来真的挺有意思。
黑洞数的计算方式是：将一组任意的数字按照一定的规则进行排列，然后计算相邻的两个数字的差值，重复这个过程，直到所有的数字都被计算过，最后得到的数字就是黑洞数。
黑洞数的产生原因是由于数字的排列方式具有一定的规律性，使得每次计算相邻的两个数字的差值都会产生循环，从而使得最后的结果与之前的结果相同。黑洞数的性质在许多数学问题中都有应用，例如在密码学、几何学等领域都有涉及。

4、勾股定理

　　重新生成：
《毕达哥拉斯定理别名：商高定理、百牛定理》是公元前551年由毕达哥拉斯、赵爽和商高等人提出的一个几何定理。该定理表明，在直角三角形中，两个直角边的平方和等于斜边的平方。使用公式a² + b² = c²可以证明这个定理。自该定理提出以来，已有数百种不同的证明方法。这个定理对今天的高考学生来说非常有用。

5、哥德巴赫猜想

　　《黄金分割猜想》别称“强哥德巴赫猜想”和“弱哥德巴赫猜想”，英文名：Golden section conjecture，是一个数学猜想。
提出者：哥德巴赫
提出时间：1742年
在说明这个猜想之前，我先科普一下什么是黄金分割。黄金分割，又称黄金比例或称黄金比，是指事物各部分间的一个数学比例关系，具体数值为1:1.61803398875。黄金分割最早由古希腊数学家欧几里得描述。其在自然界中的存在广泛，被许多动物、植物、建筑等采用。
《黄金分割猜想》最开始被提出来的版本是任何一个大于二的整数都可以拆成三个质数之和，因为哥德巴赫自己无法证明，之后有人推算到大于五、大于七最后证明了这个猜想。
哥德巴赫猜想是一道关于数论的重要问题，被数学家们称为“世纪难题”。虽然许多数学家在过去的两个世纪里对这个问题进行了大量的研究和尝试，但至今仍然未能完全证明。

6、蝴蝶定理

　　《蝴蝶原理》又被称为霍纳定理，是18世纪英国数学家W.G.霍纳提出的一种数学定理，它是平面几何学中的一种重要定理，以其独特的图形形象和丰富的解题方法而闻名。
蝴蝶原理的提出源于一个著名的平面几何问题：在一个直角三角形中，如果一条直线将直角三角形分成两个等腰三角形，那么这条直线将直角三角形的三边都分为相等的两部分。这就是著名的“蝴蝶原理”。
霍纳定理的图形形象正是由这个直角三角形的两条等腰三角形像蝴蝶的翅膀一样展开形成的。这个图形的形状随着图形的旋转而改变，但它的基本形状始终是蝴蝶的翅膀。这种图形形象直观、生动，使得霍纳定理的解题变得更加有趣和生动。
蝴蝶原理的解题方法多种多样，可以运用作图法、对称法、面积法等等，不同的解题方法可以适用于不同的题型。例如，作图法可以通过画出蝴蝶的图形来直观地理解和解决定理；对称法可以利用图形的对称性来解题；面积法则可以利用图形的面积关系来解题。
蝴蝶原理不仅是平面几何学中的一个重要定理，它还在其他数学领域有着广泛的应用，如代数学、数论等。在计算机科学中，蝴蝶原理也被用来研究算法的时间复杂度。总的来说，蝴蝶原理以其独特的图形形象和丰富的解题方法，为数学提供了新的思考和研究方向，对于推动数学的发展和应用起着重要作用。

7、拿破仑定理

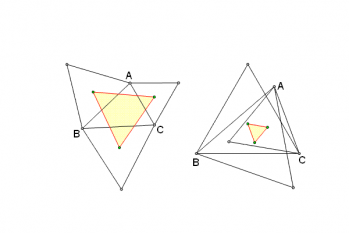
　　拿破仑三角形，又称为“三元组不等式”或“三个相等边三角形”，是一个由法国数学家拿破仑·波拿巴在1795年提出的几何问题。该问题涉及到三个等边三角形的性质，以及它们如何组成一个新的等边三角形。
在一张纸上，首先任意画一个三角形，然后以三角形的三条边向里或向外画三个等边三角形。每个等边三角形的边长与原三角形的边长相同，但是它们的边的方向可能会与原三角形的边的方向有所不同。接着，以这三个等边三角形的中心点画外接圆，连接三个中心点就是一个新的等边三角形。
拿破仑三角形的先验知识是：在一个三角形中，如果从一个顶点出发，可以引出两个互相垂直的内角平分线，那么这两个垂直平分线的交点就是这个三角形的外心。外心到各边的距离都相等，因此，以三角形的三个顶点为圆心，以外心到各边的距离为半径，恰好就可以画出三个等边三角形。
然后，根据三角形外接圆的性质，我们知道，两个互相垂直的内角平分线的交点就是三角形的外心，而外心到各边的距离都相等。因此，这三个等边三角形的中心点就是原三角形的三个顶点。这样，我们就得到了一个新的等边三角形。
在数学领域，拿破仑三角形的解法有多种，例如利用三元组不等式，利用三角形的性质等。在图形学领域，拿破仑三角形的应用也很广泛，例如在游戏开发中，可以利用该定理创建复杂的图形，提高图形的美观度和真实感。

8、四色定理

　　《四色问题》又称为四色猜想，是由英国数学家格斯里在1852年提出的。这个问题是关于平面图的颜色数的猜想，即对于任何地图，只需要四种颜色就可以将其涂色，使得相邻的区域使用不同的颜色。
这个猜想在数学界引起了广泛的关注和研究。尽管这个问题已经存在了超过160年，但至今为止，还没有一个正式的证明。四色猜想对于图论、组合数学、计算机科学等领域都具有非常重要的意义。解决这个问题可能会推动我们对于复杂图的理解和研究。
尽管四色猜想没有得到证实，但研究这个问题的方法和技巧已经被广泛地应用在其他领域，如排序算法、图像处理、网络路由等。同时，解决这个猜想也可能会带来新的数学理论和数学方法。
四色猜想的提出，体现了人类对未知的好奇心和探索精神，也是科学家们对于数学问题执着追求的体现。在科学研究中，怀疑和探索是非常重要的部分，而四色猜想就是一个很好的例子。

9、友谊定

　　友谊定理，也被称为西塔潘猜想、政治家定理和交际花定理，是由一位未知的数学家提出的。这个定理描述了一种在图形中可能存在的一种特殊结构。
友谊定理是一个关于图论的定理，图论是数学的一个分支，研究的是如何用图形和符号来表示和操作具有数学结构的事物。在每一个图中，都由一些点（称为顶点）和一些线段（称为边）组成。
友谊定理的表述是这样的：“如果一幅图中的各个顶点与相邻的顶点总是有相同的相邻的顶点，那么总有一个顶点与所有顶点相邻。”这就是说，在这样的图中，总是存在一个顶点，它与图中的其他所有顶点都有相邻的顶点。
这个定理的产生源于一个三角恋的故事。据说，这个故事中的两个男人和一个女人三个人之间存在着一种特殊的关系，这种关系就像是友谊定理中描述的那种图形结构。因此，人们将这个定理命名为“友谊定理”。
尽管这个定理听起来有些奇怪，但它实际上是图论研究中的一种重要形式，对于我们理解图的结构和性质非常有帮助。